Rpm Dalam Fisika

Hubungan Antara RPM dengan Kecepatan dan Efisiensi Bahan Bakar Terhadap Sepeda Motor

Sumber: Otomotif.kompas..com

Setelah mengetahui penjelasan tentang RPM, kamu pasti sudah mengerti ‘kan, jika kecepatan putaran mesin itu tidak langsung berhubungan dengan kecepatan yang terjadi pada putaran roda?

Angka RPM sendiri pada mesin hanya menunjukkan seberapa keras mesin kendaraan tersebut bekerja. Jadi, semakin tinggi nilai yang diraih oleh RPM tersebut, maka itu berarti semakin tinggi juga kinerja yang dilakukan mesin. Hal inilah yang kemudian menjadi patokan bagi banyak pengendara sepeda motor untuk mengetahui bagaimana kemampuan yang dimiliki oleh mesin tersebut.

Contohnya pada sepeda motor Yamaha R15 V3 yang memiliki spesifikasi daya maksimum sebesar 14,2 kW/10,000 rpm dan sepeda motor dari merek yang sama, Yamaha Vega Force yang berspesifikasi 6,14 kW/7.000 rpm.

Dari spesifikasi ini, berarti besar daya maksimum dari R15 V3 adalah 14,2 KW dalam 10.000 putaran mesin per satu menit. Sedangkan, besar output Vega Force memiliki daya maksimum 6,41 KW dalam 7.000 putaran mesin per satu menit.

Dari contoh di atas, kita dapat mengetahui jika RPM mempengaruhi daya atau tenaga yang dihasilkan oleh mesin motor, tetapi tidak mempengaruhi kecepatan motor secara langsung. Maka, semakin besar kinerja yang dilakukan pada suatu mesin sepeda motor, semakin banyak juga bahan bakar yang digunakan oleh mesin untuk melakukan putaran.

Revolutions per minute atau RPM adalah suatu unit satuan hitung yang kerap dipakai untuk menyatakan kecepatan putaran dalam satu menit. RPM dapat digunakan dalam banyak hal, termasuk mengukur kecepatan putaran pada hard disk komputer hingga perputaran kecepatan mesin pada kendaraan seperti mobil dan sepeda motor.

Meski RPM adalah singkatan dari revolutions per minute, namun masih banyak orang yang salah mengartikannya dengan rotation per minute. Kesalahan dalam mendefinisikan ini mungkin terjadi akibat dari adanya kesalahan penerjemahan dalam bahasa Inggris ke bahasa Indonesia. Tetapi pada kenyataannya, definisi yang kerap dinilai berbeda ini tetaplah sama. Sebab, RPM tetap diartikan sebagai putaran per menit yang menyatakan banyaknya putaran yang dilakukan suatu benda pada porosnya.

Itu dia rangkuman mengenai RPM yang dirangkum untuk #SahabatTanpaBatas. Sekarang, kamu sudah tahu, kan, arti dari RPM itu apa?

Jika ingin mencari buku tentang otomotif, kamu bisa mendapatkannya di Gramedia.com. Membaca banyak buku dan artikel tidak akan pernah merugikan kalian, karena Grameds akan mendapatkan informasi dan pengetahuan #LebihDenganMembaca.

Cara Menghitung Perbandingan RPM

Gambaran Umum dan Definisi

Contoh Soal Kecepatan Jarak dan Waktu

Setelah mengetahui rumus-rumus kecepatan, jarak dan waktu di atas, berikut contoh soal agar lebih paham lagi.

1. Sebuah mobil melaju dengan kecepatan tetap. Dalam waktu 3 jam, mobil tersebut menempuh jarak 210 km. Berapa kecepatan mobil tersebut? A. 80 km/jam B. 70 km/jam C. 72 km/jam D. 82 km/jam E. 76 km/jam Jawaban: B

Pembahasan dengan rumus kecepatan Jarak (S)= 210 km Waktu (t)= 3 jam Maka, dapat dihitung dengan rumus v= S/t, yakni v= 210 km/3 jam v= 70 km/jam

Dari perhitungan dengan menggunakan rumus di atas, maka didapat hasil kecepatan mobil adalah 70 km/jam

2. Sebuah kendaraan menempuh jarak 600 meter selama 5 menit, kemudian selama 10 menit berikutnya menempuh jarak 900 meter. Setelah itu, pada 750 meter terakhir waktu tempuhnya adalah 15 menit. Kecepatan rata-rata kendaraan itu adalah … A. 70 meter/menit B. 750 meter/menit C. 75 meter/menit D. 75 km/menit E. 7,5 meter/menit Jawaban: C

Pembahasan: S total = 600+900+750= 2250 meter t total= 5+10+15=30 menit Maka dapat dihitung dengan rumus v = ∆x / ∆t, yakni v= 2250 meter/30 menit v= 75 meter/menit

Dari perhitungan dengan menggunakan rumus di atas, maka didapat hasil kecepatan rata-rata mobil ada 75 meter/menit

3. Sebuah mobil melaju dengan kecepatan tetap. Berdasarkan speedometer, kecepatan laju mobil tersebut adalah 90 km/jam, selama 12 menit. Maka, berapa jarak yang ditempuh selama selang waktu tersebut? A. 12 km B. 15 km C. 14 km D. 18 km E. 16 km Jawaban: D

Pembahasan: v= 90 km/jam = 25 m/detik t= 12 menit = 720 detik Maka dapat dihitung dengan rumus S = v x t, yakni S= 25 m/detik x 720 detik S= 18.000 meter = 18 km

Dari perhitungan menggunakan rumus di atas, maka didapat hasil jarak yang ditempuh mobil tersebut adalah 18 km.

4. Sebuah truk melaju dengan kecepatan 70 km/jam. Truk akan menempuh jarak sejauh 140 km. Maka, berapa lama waktu yang dibutuhkan truk tersebut untuk sampai ke tempat tujuan? A. 1 jam 15 menit B. 1 jam 30 menit C. 2 jam D. 2 jam 25 menit E. 3 jam Jawaban: C

Pembahasan dengan rumus kecepatan S= 140 km v= 70 km/jam Maka dapat dihitung dengan rumus t = S/v, yakni t= 140 km/70 km/jam t= 2

Dari perhitungan dengan rumus di atas, maka didapat hasil waktu yang dibutuhkan truk tersebut adalah 2 jam.

5. Alia mengemudikan mobil dari rumah ke kantor yang berjarak sekitar 30 km dengan waktu 2 jam di perjalanan. Maka berapakah kecepatan dari mobil doni tersebut?

Diketahui: s = 30 km t = 2 jam Ditanya: v Dijawab: V = s/t V = 30 km/2 jam V = 15 km/jam Jadi, kecepatan dari mobil Alia adalah 15 km/jam.

6. Surya berjalan kaki dengan kecepatan rata-ratanya 2 meter per detik. Jadi, berapa jarak yang ditempuh Surya usai berjalan kaki selama 2 jam?

Diketahui: v = 2 meter/detik t = 2 jam = 2 x 60 x 60 = 7200 detik. Ditanya: s Dijawab: s = v x t s = 2 meter/detik x 7200 detik s = 14.400 meter = 14,4 km Jadi, jarak yang ditempuh Surya usai berjalan kaki selama 2 jam adalah 14,4 km.

7. Sebuah pesawat terbang dengan kecepatan 500 km/jam. Berapa lama waktu untuknya terbang dari kota A ke kota B apabila jarak kedua kota itu adalah 1.500 kilometer?

Diketahui: s = 1.500 km v = 500 km/jam Ditanya: t dari kota A ke kota B Dijawab: t = s/v t = 1500 km/500 km/jam t = 3 jam Jadi, waktu yang dibutuhkan pesawat itu untuk terbang kota A ke kota B adalah 3 jam.

8. Wildan mengendarai mobil dengan dari kota A ke kota B yang berjarak sekitar 20 km selama 2 jam lalu melanjutkan perjalanan 40 km menuju kota C selama 3 jam. Berapa kecepatan rata-rata yang telah ditempuh mobil Wildan?

Diketahui: s2-s1 = 40 km – 20 km = 20 km t2 – t1 = 3 jam – 2 jam = 1 jam Ditanya: kecepatan rata-rata Dijawab: v = (s2 – s1) / (t2 – t1) = 20 km/jam Jadi, kecepatan rata-rata yang telah ditempuh mobil Wildan adalah 20 km/jam.

9. Jarak Yogyakarta-Magelang adalah 195 km. Jika ditempuh menggunakan mobil dengan kecepatan 65 km/jam. Berapa waktu yang diperlukan untuk menempuh jarak tersebut?

Jawab: Diketahui: s = 195 km; v = 65 km/jam. Ditanya: Waktu atau t. t = s ÷ v t = 195 ÷ 65 t = 3 Jadi, waktu yang dibutuhkan untuk menempuh jarak dari Yogyakarta-Magelang adalah 3 jam.

10. Seorang pelari cepat bergerak lurus beraturan dalam waktu 5 sekon. Ia dapat menempuh jarak 40 meter. Kecepatan rata-rata pelari itu adalah …

Jawab: Diketahui: Δs = 40 m, Δt = 5 s. v = Δs/Δt v = 40/5 = 8 m/s Jadi, kecepatan rata-rata pelari tersebut adalah 8 m/s.

11. Pelari atletik mampu menempuh jarak 200 meter dalam rentang waktu 25 detik. Berapakah kecepatan rata-rata pelari tersebut?

Jawab: Jarak tempuh = 200 m Waktu tempuh =25 detik Kecepatan rata-rata = 200/25 = 8 m/detik.

12. Motor vespa menempuh jarak 110 kilometer dalam kurun waktu 2 jam. berapakah kecepatan rata-rata motor vespa tersebut.

Jawab: Jarak tempuh = 110 km Waktu tempuh =2 jam Kecepatan rata-rata = 110/2 = 55 km/jam.

13. Doni mengendarai mobil nya dari rumah ke kantor yang berjarak sekitar 25 km dengan waktu 2 jam di perjalanan. Jadi berapakah jumlah kecepatan rata-rata mobil tersebut?

Jawab: Diketahui: S = 25 km t = 2 jam

Ditanya: kecepatan rata-rata (v) ….. ?

Dijawab: V = S / t V = 25 km / 2 jam V = 12,5 km/jam Maka, kecepatan mobil itu ialah 12,5 km/jam.

14. Pada saat Dono berlari diperkirakan dengan kecepatan rata-ratanya 1,5 meter per detik. Jadi, hitung jumlah jarak yang ditempuh oleh Doni setelah 2 jam perjalanan?

Jawab : Diketahui: v = 1,5 meter/detik t = 2 jam = 2 x 60 x 60 = 7200 detik.

Ditanya: Jadi berapa jumlah jarak yang dapat ditempuh oleh Doni setelah 2 jam berjalan (s) ?

Dijawab: s = v x t s = 1,5 meter/detik x 7200 detik s = 10800 meter = 10,8 km Jadi, jarak yang ditempuh oleh Doni setelah 2 jam berjalan ialah 10,8 km.

15. Ada pesawat yang ang diperkirakan dengan kecepatan 500 km/jam. Jadi, berapakah waktu yang dibutuhkan pesawat tersebut untuk terbang dari Bandar Lampung ke Bandung bila jarak kedua kota tersebut ialah 1400 kilometer ?

Jawab: Diketahui: S = 1400 km v = 500 km/jam

Ditanya: Diketahui waktu yang dibutuhkan pesawat terbang dari Bandar Lampung ke Bandung (t)?

Dijawab: t = s / t t = 1400 km / 500 km/jam Jadi, waktu yang dibutuhkan pesawat garuda indonesia untuk terbang dari Bandar Lampung ke Bandung ialah 2 jam 48 menit.

16. Vishal mengayu sebuah sepeda dengan kecepatan 2 m/s. Maka berapa lama waktu yang diperlukan vishal dalam menempuh jarak 100 meter?

Jawab: Diketahui: v = 2 m/s s = 120 m

Penyelesaian: t = s / v t = 100 / 2 t = 50 sekon Jadi, waktu diperlukan vishal adalah 50 sekon

17. Diketahui Ilham mengendarai sebuah sepeda motor dengan menempuh jarak 100 meter dengan waktu 25 detik. Maka berapakah kecepatan motor-motoran Ilham?

Jawab: Diketahui: s = 100 m t = 25 s

Ditanya v ….? Penyelesaian: v = s / t v = 100 / 25 v = 4 m/s Jadi, kecepatan motor-motoran vishal adalah 4 m/s

18. Apabila telah diketahui pada jarak X – Y ialah 33 km. Kemudian seorang Adik pergi dari X pukul 09.00 dengan kecepatan perjam 6 km. Dan pada kakaknya tersebut diperkirakan berangkat dari B pukul 09.00 dengan kecepatan perjam 5 km. Pukul berapakah kakak dan adik akan bertemu ?

Pembahasan: Gunakanlah rumus untuk menghitung jarak: s = v . t Jarak Adik + Jarak Kakak = 33 km 6 km . t + 5 km . t = 33 km 11 t = 33 t = 3 jam Jam mereka akan bertemu = 09.00 + 3 jam = 12.00 Jadi, Adik dan Kakak akan bertemu pada pukul 12.00

19. Jarak Bekasi–Jakarta 60 km. Angga berangkat ke Jakarta dengan sepeda mobil pukul 07.30. Kecepatan rata-rata angga ialah 40 km/jam.

Hitunglah: a. Berapa waktu tempuh yang dibutuhkan oleh Angga untuk sampai ke Jakarta ? b. Pukul Berapakah Angga tiba di Jakarta?

Jawaban: a. kita peruganakan Rumus untuk menghitung waktu tempuh ialah t=s/v atau = Jarak : kecepatan = 60 km : 40 km/jam = 1,5 jam

Maka berapakah waktu yang dibutuhkan untuk menempuh jarak Bekasi–Jakarta ialah 1,5 jam = 1 jam 30 menit.

b. Tibanya Angga di Jakarta = Waktu pergi+ waktu tempuh = pukul 07.30+ pukul 01.30 = 09.00 Jadi, Angga tiba di Jakarta pukul 09.00

20. Karno mengendarai ssebuah mobil dengan kecepatan rata-rata 60 km/jam. Dari Jakarta hingga menuju kota Bandung ia berangkat pada pukul 04.00. Apabila Karno sampai di kota Bandung Pukul 07.00. Berapa Km jarak yang telah ditempuh Karno ?

Jawab : Keterangan Rumus jarak tempuh s=vxt Waktu tempuh dan = waktu tiba kemudian – waktu berangkat = Pukul 07.00 – Pukul 04.00 = 3 jam

Jarak yang ditempuh = kecepatan X waktu = 60 km/jam X 3 jam = 180 km Maka Karno sudah menempuh jarak 180 km

21. Jarak antara Jakarta–Bogor adalah 60 km. Rossa berangkat ke Bogor dengan sepeda motor pukul 07.30. Kecepatan rata-rata Rossa adalah 40 km/jam.

Pertanyaan: a. Agar sampai ke bogor maka berapakah waktu tempuh yang diperlukan Rossa ? b. Pukul Berapakah Ross tiba di Bogor?

Jawab: a. Rumus menghitung waktu tempuh adalah t=s/v atau = Jarak : kecepatan = 60 km : 40 km/jam = 1, 5 jam Jadi Rossi membutuhkan waktu untuk menempuh jarak dari Jakarta ke Bogor yaitu. 1,5 jam = 1 jam 30 menit.

b. Tiba di Bogor = Waktu saat keberangkatan + kemudian waktu tempuh = pukul 07.30+ pukul 01.30 = 09.00 Maka Rossa tiba di Bogor pukul 09.00. — Itu tadi penjelasan tentang rumus kecepatan, jarak dan waktu beserta contoh soalnya. Sekarang sudah paham kan dengan rumus kecepatan dan cara menghitungnya? Semoga informasi tadi membantu!

Jenis-Jenis Kecepatan

Kecepatan Rambat Gelombang

Kecepatan rambat gelombang adalah kecepatan yang mengukur berapa cepat pola osilasi berpindah dari satu tempat ke tempat yang lain. Kecepatan rambat gelombang mengukur berapa cepat sebaran gelombang arah radial keluar meninggalkan titik jatuhnya batu yang dilakukan pada permukaan air.

Beberapa satuan kecepatan lainnya adalah:

Perubahan kecepatan tiap satuan waktu dikenal sebagai percepatan atau akselerasi.

Fisika Kuantum Edisi 2 Revisi

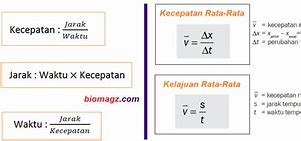
Rumus Kecepatan Rata-Rata – Kecepatan adalah perpindahan yang ditempuh oleh manusia maupun sebuah benda di dalam jangka waktu tertentu yang dinyatakan di dalam satuan meter per sekon (satuan ukuran panjang per satuan ukuran waktu). Untuk mengetahui kecepatan, maka dibutuhkan jarak yang nantinya akan dibagi dengan waktu. Di bawah ini adalah rumus kecepatan, rumus kecepatan rata-rata, rumus untuk menghitung jarak, dan rumus untuk menghitung waktu beserta contoh pengerjaannya yang dilansir dari buku Kumpulan Rumus Terlengkap Matematika-Fisika-Kimia: (Chapter 2 Fisika), Wahyu Utama, (2015:166).

Rumus kecepatan, jarak dan waktu biasa dipelajari dalam pelajaran IPA atau Fisika. Rumus ini biasanya digunakan untuk menentukan besaran waktu perpindahan suatu objek dari satu tempat ke tempat lainnya, misalnya perpindahan mobil. Kecepatan merupakan perpindahan yang ditempuh tiap satuan waktu oleh suatu benda. Kecepatan dalam ilmu fisika terbagi menjadi dua, yakni kecepatan rata-rata dan kecepatan sesaat.

Dari rumus kecepatan, biasanya kita juga bisa menentukan waktu dan juga jarak. Lalu, apa rumusnya? Dan bagaimana contoh soal serta cara menjawabnya? Simak penjelasannya berikut ini.

Kecepatan merupakan besaran turunan yang diturunkan dari besaran pokok panjang dan waktu, dimana rumus kecepatan yaitu jarak dibagi waktu. Kecepatan besaran vektor yang menunjukkan seberapa cepat benda berpindah. Besar dari vektor ini disebut dengan kelajuan dan dinyatakan dalam satuan meter per sekon (m/s atau ms−1).

Kecepatan biasa digunakan untuk merujuk pada kecepatan sesaat yang didefinisikan secara matematis sebagai:

di mana adalah kecepatan sesaat pada waktu dan adalah fungsi perpindahan terhadap waktu.

Selain kecepatan sesaat, dikenal juga besaran kecepatan rata-rata yang didefinisikan dalam rentang waktu yang tidak mendekati nol.

Kecepatan ditulis dalam bentuk vektor untuk dimensi dua dan keatas, untuk kecepatan dalam dimensi 1, umumnya kecepatan hanya ditulis .

Penulisan vektor kecepatan:

Besar dari vektor kecepatan adalah kelajuan dan tidak seperti kecepatan, kelajuan tidak memiliki arah dan hanya memiliki besar tak negatif.

Kecepatan Rambat Gelombang

Beberapa satuan kecepatan lainnya adalah:

Perubahan kecepatan tiap satuan waktu dikenal sebagai percepatan atau akselerasi.

Kecepatan Rata-Rata

Kecepatan rata-rata merupakan perbandingan antara perpindahan yang terjadi pada sebuah benda dengan waktu yang diperlukan untuk melakukan perpindahan. Dalam kecepatan rata-rata, bentuk lintasan dan cara bergerak dari benda tidak diperhitungkan. Data yang diperlukan dalam pengukuran kecepatan rata-rata adalah posisi awal, posisi akhir dan waktu tempuh.

Kecepatan osilasi adalah kecepatan yang mengukur berapa cepat perubahan simpangan titik-titik pada medium. Kecepatan osilasi mengukur berapa cepat gerakan naik dan turun simpangan pada gelombang transversal. Sedangkan untuk gelombang longitudinal, kecepatan osilasi mengukur berapa cepat getaran maju mundur titik-titik dalam medium.

Rekomendasi Buku Terkait Pengertian Jarak

Jarak vs Jarak Terarah dan Perpindahan

Baik jarak dan perpindahan sama-sama mengukur pergerakan suatu benda. Jarak adalah besaran skalar sedangkan perpindahan adalah besaran vektor dengan besar dan arah. Jarak kedua titik tidak dapat bernilai negatif. Di sisi lain, karak terarah tidak mengukur pergerakan; itu mengukur posisi sebuah titik dari suatu titik acuan, dan dinyatakan dalam bentuk vektor.

Jarak yang ditempuh oleh kendaraan (misalnya seperti yang dicatat oleh odometer), orang, hewan, atau objek di sepanjang lintasan melengkung dari titik A ke titik B harus dibedakan dari jarak garis lurus dari A ke B, karena secara umum jarak garis lurus tidak sama dengan jarak yang ditempuh, kecuali untuk perjalanan dalam garis lurus.

Jarak terarah dapat ditentukan di sepanjang garis lurus dan di sepanjang lintasan melengkung. Jarak terarah sepanjang garis lurus adalah vektor yang memberikan informasi jarak dan arah antara titik awal dan titik akhir. Jarak terarah titik dari titik pada garis dan dalam arah pada ruang vektor Euklides adalah jarak dari ke jika jatuh pada sinar , tetapi bernilai negatif jika jatuh pada sinar .

Jarak terarah sepanjang lintasan melengkung bukanlah vektor dan diwakili oleh segmen garis lengkung yang ditentukan oleh titik ujung A dan B, dengan beberapa informasi spesifik yang menunjukkan pengertian (atau arah) gerakan ideal atau nyata dari satu titik ujung lintasan ke yang lain. Misalnya, hanya memberi A dan B sebagai label dua titik dapat menunjukkan pengertian, jika urutan (A, B) menyiratkan bahwa A adalah titik awal.

Perpindahan adalah kasus spesial jarak terarah yang terdefinisi di mekanika. Jarak terarah disebut perpindahan jika lintasan antara titik A dan B berupa garis lurus (jarak terpendek antara A dan B).